티스토리 뷰
목차
1. Trie란?
2. Trie의 특성
3. Trie의 장단점
4. 구현 코드
5. 사용 예시
1. Trie란?
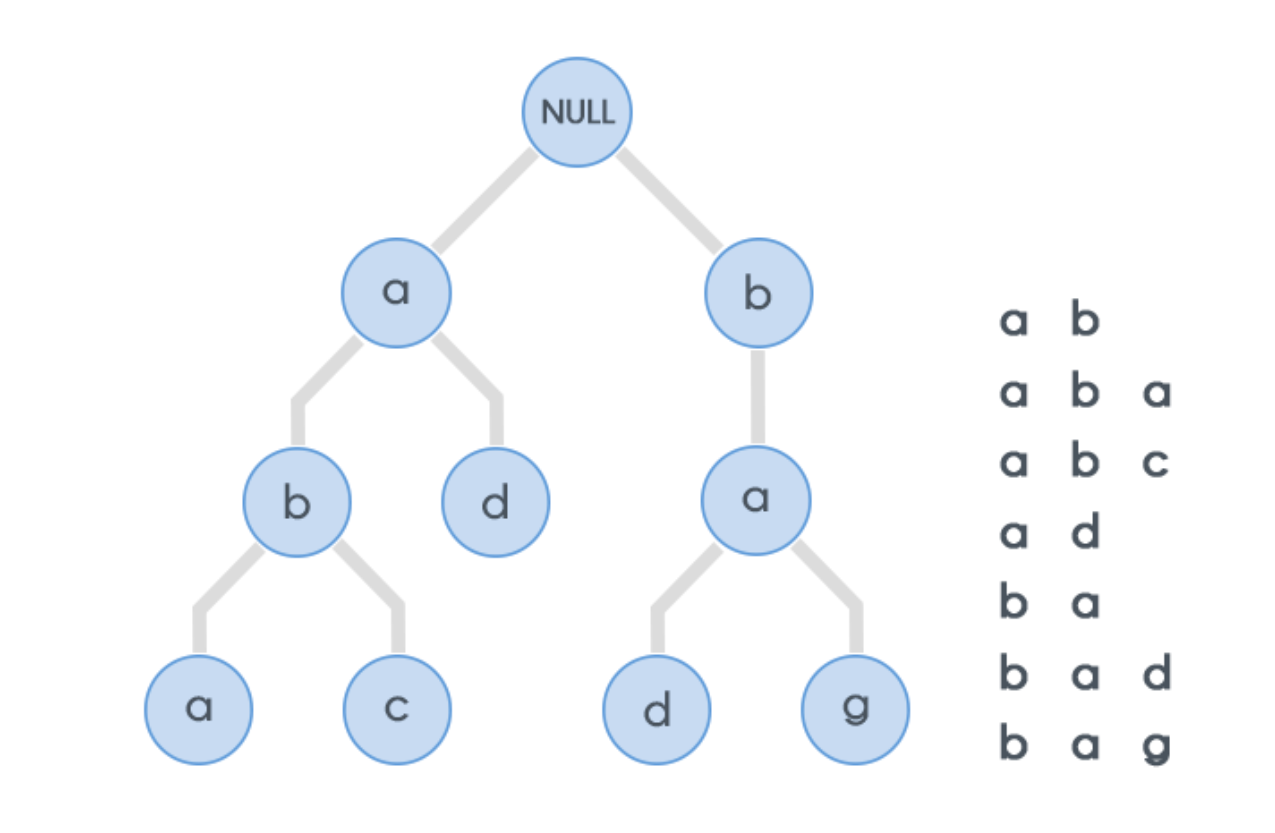
- 탐색 트리의 일종으로 동적 집합이나 연관 배열을 저장하는 데 사용됨
- Digital Tree, Radix Tree, Prefix Tree라고도 불림
- 텍스트 자동 완성 기능과 같이 문자열을 저장하고 탐색하는 데 유용
2. Trie의 특성
- 이진 탐색 트리와 달리 트리의 어떤 노드도 그 노드 자체와 연관된 키는 저장하지 않음
- <key, value> 형태의 맵이다
- key는 주로 문자열이다
- value는 key에 해당하는 자식 노드이다.
- 키의 값은 자료 구조 전체에 분산된다
- 노드의 모든 자손은 노드에 연관된 문자열의 공통 접두사를 공유한다
- 루트 노드는 빈 문자열이며 자식 노드만 가지고 있다
- 문자열의 길이가 m일 때, 탐색과 삽입 모두 시간복잡도는 O(m)이다
3. Trie의 장단점
장점
- 해시테이블을 대체할 수 있다.
- 키 충돌이 일어나는 불완전한 해시 함수에 비교했을 때 더 작은 시간 복잡도를 갖는다.
- 트라이에서는 키 충돌이 일어나지 않는다.
- 해시 함수가 없어도 되며 키의 개수가 늘어난다고 해시 함수를 변경할 필요가 없다
- 모든 항목에 따라 사전순으로 정렬된다
단점
- 해시 테이블보다 조회가 느릴 수 있다.
- 특히 보조 기억장치에서 직접 읽을 때
- 메모리를 비교적 많이 소비한다. 검색 문자열의 각 문자마다 메모리가 할당될 수 있다.
4. 구현 코드
정의, 탐색, 삽입, 삭제
# 출처 : 위키피디아
class Node:
def __init__(self):
self.children: Dict[str, Node] = {}
self.value: Optional[Any] = None
# 탐색
# key에 대응하는 문자열을 검색
# key의 문자열의 문자들(알파벳)에 해당하는 노드를 찾으면 그 자식노드를 검색함
def find(node: Node, key: str) -> Optional[Any]:
for char in key:
if char in node.children:
node = node.children[char]
else:
return None
return node.value
# 삽입
# <key, value>를 삽입
# 트라이에 이미 포함된 문자를 찾아감
# 포함되지 않으면 나머지 문자를 새 노드로 만들어 붙임
def insert(node: Node, key: str, value: Any) -> None:
for char in key:
if char not in node.children:
node.children[char] = Node()
node = node.children[char]
node.value = value
# 삭제
# lazy하게 삭제할 수도 있고, eager하게 삭제할 수도 있음
# 아래는 조급하지 않은 (eager) 삭제 코드
def delete(root: Node, key: str) -> bool:
def _delete(node: Node, key: str, d: int) -> bool:
"""
키[d]에 해당하는 노드를 비우고 하위 트라이가 비었으면 자식 key[d+1]를 삭제하고,
node가 비었는지 반환
"""
if d == len(key):
node.value = None
else:
c = key[d]
if c in node.children and _delete(node.children[c], key, d+1):
del node.children[c]
# Return whether the subtrie rooted at `node` is now completely empty
return node.value is None and len(node.children) == 0
_delete(root, key, 0)
자동완성
def keys_with_prefix(root: Node, prefix: str) -> List[str]:
results: List[str] = []
x = _get_node(root, prefix)
_collect(x, list(prefix), results)
return results
def _collect(x: Optional[Node], prefix: List[str], results: List[str]) -> None:
"""
주어진 접두사 `prefix`에 해당하는 노드 `x` 아래의 키를 `results`에 추가
"""
if x is None:
return
if x.value is not None:
prefix_str = ''.join(prefix)
results.append(prefix_str)
for c in x.children:
prefix.append(c)
_collect(x.children[c], prefix, results)
del prefix[-1] # delete last character
def _get_node(node: Node, key: str) -> Optional[Node]:
"""
key 키로 노드를 탐색. 앞에서 정의한 `find` 함수와 같지만, 찾은 노드의 값 대신 노드 자체를 반환.
"""
for char in key:
if char in node.children:
node = node.children[char]
else:
return None
return node
5. 사용 예시
- 검색 자동 완성 예측
- 맞춤법 검사
참고 문헌
github : Woovictory/Ready-For-Tech-Interview
GitHub - WooVictory/Ready-For-Tech-Interview: 💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간
💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간 👨💻. Contribute to WooVictory/Ready-For-Tech-Interview development by creating an account on GitHub.
github.com
트라이 (컴퓨팅) - 위키백과, 우리 모두의 백과사전
"A", "to", "tea", "ted", "ten", "i", "in", "inn"를 키로 둔 트라이. 이 예제에는 모든 자식 노드가 알파벳 순으로 왼쪽에서 오른쪽으로 정렬되어 있지는 않다. (루트 노드와 't' 노드) 트라이(trie)는 컴퓨터
ko.wikipedia.org
https://vishalkhatal.wordpress.com/2020/08/01/trie/
Trie
A Trie is a special data structure used to store strings that can be visualized like a graph. It consists of nodes and edges. Each node consists of at max 26 children and edges connect each parent …
vishalkhatal.wordpress.com
'CS' 카테고리의 다른 글
| 이진검색 트리 (Binary Search Tree) (0) | 2022.05.02 |
|---|---|
| Tree (0) | 2022.05.02 |
| Stack vs Queue (0) | 2022.05.02 |
| Array vs Linked List (0) | 2022.05.01 |
| Map (0) | 2022.04.20 |
